ひずみゲージによる測定とは？

ひずみゲージは長さの物理量を”１００万分の１”の変化レベルを容易に測定できる極めてユニークなセンサーです。 1938年にアメリカにおいて”Simmons & Ruge” により考案されたもので、株式会社昭和測器では1962年、わが国で始めて箔ひずみゲージとして製造を開始し既に４５年を経過しております。このひずみゲージは一般的には馴染みが薄い「金属・ゴム・プラスチック・セラミック等」の各種材料の応力／ひずみ測定による物性評価に利用されておりますが、このひずみゲージによる測定の原理を知ることで専門的な知識なしでより身近な問題に対する解決手段としてご利用して頂けると考えております。

ひずみゲージによる測定は”１００万分の１”の世界

ひずみゲージは長さの物理量を”１００万分の１”の変化レベルで測定可能と述べましたが、一般の長さ測定においては、例えば、100mの長さのものを0.1mm の正確さで測ることは非常に困難です。しかし、ひずみゲージでは”0.3～5mm”の長さの抵抗線が外力を受けることにより、ΔL／L∝ΔR／R から、長さに比例した抵抗変化ΔRを電気的なホイートストンブリッジを介し”１００万分の１”の世界を捉えることが可能になります。

ひずみゲージによる測定の目的

ひずみゲージは局部的な長さ変化ΔLを検出しているが、実際にはこの変形量から導き出される物理量である応力、外力、圧力等に置きかえて評価することが一般的です。また、一般に市販されているひずみゲージは自己温度補償ゲージであることから、未知の線膨張係数の測定への応用も考えられます。

知っておきたいひずみゲージに関連した用語および式

ひずみの定義：ε＝ΔL/L ・ゲージ率：ΔR/R＝K*ε
垂直応力とひずみの関係：σ＝E*ε
剪断応力と剪断ひずみの関係：τ＝G*γ
垂直応力の計算式：σ＝P/A
はりの曲げによる表面応力の計算式：σ＝M/Z＝6M/bh^2 （Z：断面係数）
丸棒のねじりによる剪断応力の計算式：τ＝T/Zp＝（Zp：極断面係数）
- ・中軸断面（Zp）：π*d^3/16
- ・中空断面（Zp）：π*(d2^4－d1^4)/16*d2）
縦弾性係数／Eと横弾性係数／G の関係：G＝E/2(1＋ν)
ゲージ率(gage factor)／K：ひずみと抵抗変化の間に直線的な関係がある時の比例定数
ポアソン比／ν：垂直応力”σ”による縦ひずみ”ε”と、それと同時に生じる横ひずみ”εb”の比で材料定数
垂直応力(stress)／σ：単位面積あたりの内力
弾性限度(elastic limit)／降伏点(yield point)：”σ”と”ε”が直線的な関係にある時の最大応力
縦弾性係数(modulus of elasticity)／E：σとεが直線的な関係にある時の比例定数
横弾性係数(modulus of transverse elasticity)／G：τとγが直線的な関係にある時の比例定数

自己温度補償ゲージ(self-temperature compensated gage)

抵抗体であるゲージが１℃ 当たり抵抗値の相対的変化した場合、 ΔR／R＝α＋K(βs－βg) で表されることから、 0＝α＋K(βs－βg) の関係式が成立すれば温度による影響がないことになる。ここで、ゲージ抵抗材料／アドバンス（Cu54,Ni45,Mn1）の抵抗温度係数／”α”は熱処理によりコントロールすることが出来ることから被測定材料の線膨張係数にマッチした「見かけひずみ」の少ないひずみゲージを製作することが可能になります。尚、一般に市販されているひずみゲージは自己温度補償ゲージ（適用母材：鉄、ステンレス、アルミ）が主流です。 α ：ゲージ抵抗材料の抵抗温度係数Ｋ：ゲージ率 βs：被測定材料の線膨張係数 βg：ゲージ抵抗材料の線膨張係数

ひずみゲージの温度特性／熱出力（サンプルゲージ：N11-MA-5-120-11）

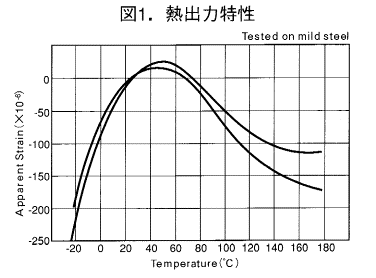図１は、当社の自己温度補償形ひずみゲージの温度による見かけ出力曲線で、２曲線の幅に相当するするのがバラツキを示し、ダミーゲージ無しで±2μstrain以内／℃（常温付近）に補償されてます。

ひずみゲージの温度特性／ゲージ率変化（サンプルゲージ：N11-MA-5-120-11）

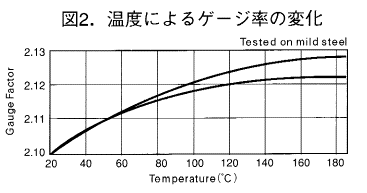図２に示した特性は”鋼”にひずみゲージを貼付け、＋1000μstrain／20℃ で一定ひずみを加え温度を変化させた場合のゲージ感度変化を表した曲線である。注）この曲線は”鋼”のヤング率変化を含めています。

応力・ひずみ曲線

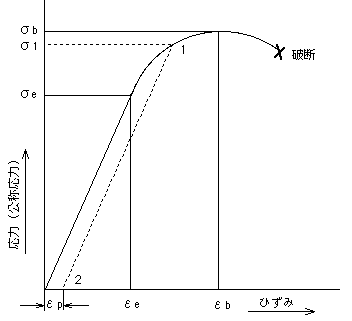σe：弾性限度(elastic limit)／降伏点(yield point) σb：極限応力(ultimate stress) 注）引張の場合は”引張強さ(tensile strength)”と呼ばれる εp ：永久ひずみ(permanent set) Ｅ：縦弾性係数(modulus of elasticiy)又はヤング率(Young’s modulus)と呼び、応力／ひずみの直線範囲での傾きに相当し、E=σ/εで表される。参考） σ1：永久ひずみが残った状態ににおいて新たに負荷を加えた場合、曲線２－１をたどり新たな降伏点 σ1となる。すなわち、塑性変形することにより降伏点が変化するが材料は「こわく」かつ「もろく」なる。

ブリッジの一辺に並列抵抗挿入による簡単な等価ひずみ発生法

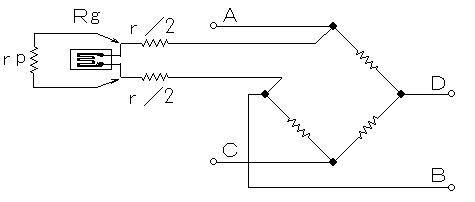ひずみゲージのリード線又はブリッジボックス～アンプ間ケーブルが数十ｍと長い場合は、リード線抵抗による感度変化の影響が大きくなりますので、正確な較正値（等価ひずみ）の発生させる方法として下図のようにひずみゲージに並列抵抗（ｒp）を挿入します。尚、較正ひずみ（ε）、挿入抵抗（ｒp）とゲージ抵抗（Ｒg）は次式の関係になります。Ｒg/(ｒp＋Ｒg)＝K*ε　から　ｒp≒Ｒg/(K*ε) 例）ブリッジ抵抗／Ｒg：120Ω、K：2.00 のとき、較正ひずみ2000×10-6を発生させる場合、上記計算式より挿入抵抗値は30kΩとなります。また、ひずみ計測範囲に応じて外部CAL抵抗を用意されると良いでしょう。

引張り及び圧縮応力の計測＜１ゲージ法＞

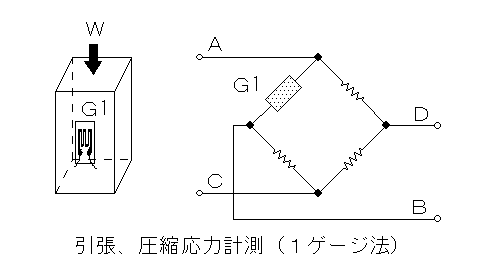図の様に一方向から均一な力を受けている柱の表面に、力の方向と平行にひずみゲージを一枚接着した場合の応力（σ）及び力（W）は次式で表される。 σ＝εo*Ｅ σ ：応力Ｅ：縦弾性係数（ヤング率） εo：指示ひずみ W＝Ａ*σ＝Ａ*εo*Ｅ W：材料に加えた力Ａ：材料の断面積

引張り及び圧縮応力の計測＜２ゲージ法（Ａ）＞

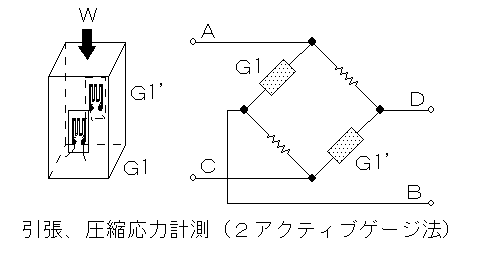図の様に両面に、力の方向と平行にひずみゲージを接着した場合の応力（σ）及び力（W）は次式で表される。 σ＝(1/2)*εo*Ｅ W＝Ａ*σ＝Ａ*(1/2)*εo*Ｅ W＝Ａ*σ＝Ａ*(1/2)*εo*Ｅ W＝Ａ*σ＝Ａ*εo*Ｅ W：材料に加えた力Ａ：材料の断面積また、指示ひずみ（εo）は曲げひずみは打ち消され、軸ひずみ（ε）の平均化された２倍の出力となります。

引張り及び圧縮応力の計測＜２ゲージ法（Ｂ）＞

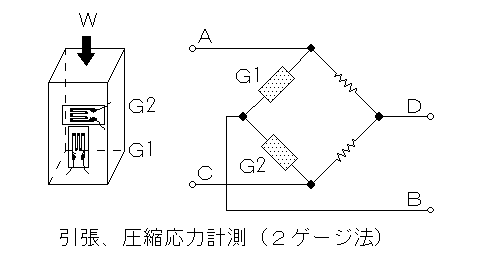力の方向とそれと直角の方向にひずみゲージを接着し、下図の様に接続しますと柱の応力（σ）及び力（W）は次式で表される。 σ＝εo*Ｅ/(１＋ν) W＝Ａ*σ＝Ａ*εo*Ｅ/(１＋ν) ν：ポアソン比また、指示ひずみ（εo）は、ε1とε2（＝－νε1）の絶対値として出力されます。

曲げ応力の計測＜１ゲージ法＞

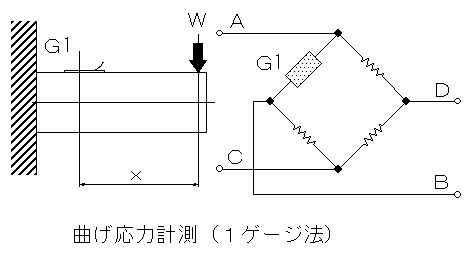一端を固定し、他端に力を加えた矩形断面の片持ち梁の表面にひずみゲージを１枚接着した時のひずみゲージ接着位置の表面応力（σ）は σ＝εo*Ｅ加えた力（Ｗ）によるモーメントＭは、Ｍ＝Ｗ*X X ：力を加えた位置からひずみゲージ中心までの距離梁の表面応力（σ）及びひずみ（εo）は次式で表される。 σ＝Ｍ/ＺＭ＝Ｚ*εo*ＥＺ：梁の断面係数矩形断面の場合の断面係数は、Ｚ＝ｂ*ｈ^2/6から、ひずみ（εo）と梁に加えた力（Ｗ）の関係は次式で表される。Ｗ＝ｂ*ｈ^2*Ｅ*εo/６*X ｂ：梁の幅ｈ：梁の厚さ

曲げ応力の計測＜２ゲージ法＞

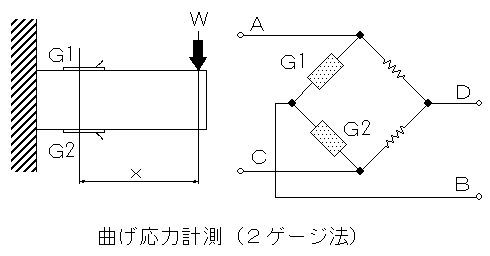梁の裏表対称位置にひずみゲージを接着するとひずみゲージの出力は絶対値が等しく、符号が逆になります。このひずみゲージを隣辺どうしになるように接続しますと、曲げひずみは２倍になり、軸方向の力によるひずみは打ち消されます。この時の応力は、 σ＝εo*Ｅ/２で表されます。

剪断応力の計測

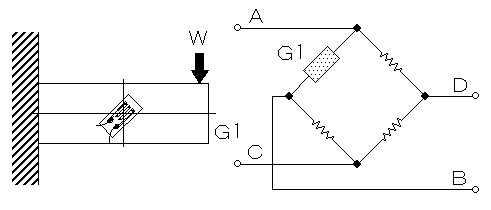剪断応力（τ）は τ＝Ｆ/ＳＦ：剪断力Ｓ：梁の断面積この場合の剪断力はＦ＝Ｗになり梁の断面積はＳ＝ｂ*ｈから剪断応力（τ）は次式で表される。 τ＝Ｗ/ｂ*ｈｂ：梁の巾ｈ：梁の厚さまた、剪断応力（τ）と剪断ひずみ（γ）の関係は τ＝Ｇ*γ Ｇ：横弾性係数から γ＝Ｗ/Ｇ*ｂ*ｈとなる。また、剪断ひずみγ（rad）は、45°方向のひずみεoの２倍に相当することから、εoを求めることにより剪断応力（τ）及び剪断力（Ｗ）を求めることが出来る。 γ＝2*εo τ＝2*Ｇ*εo Ｗ＝2*Ｇ*ｂ*ｈ*εo

ねじり応力の計測

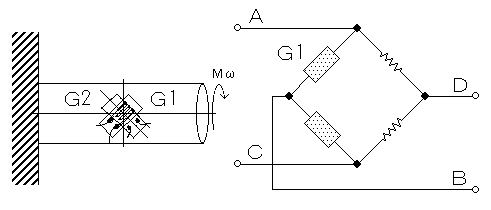図の様にねじりモーメント（Ｍω）を受けている軸では剪断応力は軸表面で最大となりその値は、 τmax＝Ｍω/Ｚp Ｚp：極断面係数となり表面剪断ひずみγは、 γ＝τmax/Ｇ＝Ｍω/Ｇ*Ｚp また、γ＝2*εoから２ゲージ法で計測するとその指示ひずみ（εo’）が表面剪断ひずみの値となり、剪断応力（τ）とねじりモーメント（Ｍω）は次式で表せる。 τmax＝Ｇ*εo’ εo’＝γ＝2*εo Ｍω＝Ｇ*Ｚp*εo’

PRODUCTS